
The points where the line segments intersect are called vertices. Edges are also called sides, and they are nothing but the line segments which make up the polygons. The polygons are classified by the number of edges they have. There are many different types of polygons, some of them being triangles, quadrilaterals, pentagons hexagons etc. Some examples of rectangle shapes are- mobile screens, blackboard, doors, etc.Īny closed shape made up of at least three-line segments is known as a polygon. The area of a shape is measured in terms of the number of square units such as square feet, square inch, square centimeters and so on. Therefore, the area of a rectangle is equal to the number of unit squares that can fit into the boundaries of a rectangle. The number of unit squares that can fit into any shape, is the area of that shape. Try out the practice question to further your understanding.A quadrilateral whose parallel sides are equal to each other and all the vertices are perpendicular to each other is called a rectangle. Since the width is in feet, the length will also be in feet.įinally, the length of this rectangle is 7ft. Note that, this number doesn't mean anything, unless we include the unit for it. To do so, we add -5 to both sides of the equation.īy doing so, we get, L equals to 12 minus 5. Let's rewrite this equation so that it looks neater.
#PERIMETER OF A RECTANGLE PLUS#
This gives, 24 over 2, equals to L plus 5. To do so, we divide both sides of the equation with 2. Now, to get a step closer in finding L, we need to remove '2'. Similarly, since the width is given as 5ft, we can substitute W with 5. Since the perimeter, and the width of the rectangle are given, we can find the length of the rectangle, by solving this equation for L. Find its length.Īgain, we start with the formula for the perimeter of a rectangle, P=2(L+W). Next example, the perimeter of this rectangle, is 24ft, and its width is 5ft. Therefore, the perimeter of this rectangle is equals to 14cm.

Since the length, and the width, are given in centimeter, the unit for the perimeter will also be in centimeter. Now, this number doesn't mean anything, unless we include the unit for it. Similarly, since the width is given as 3cm, we can substitute W with 3.
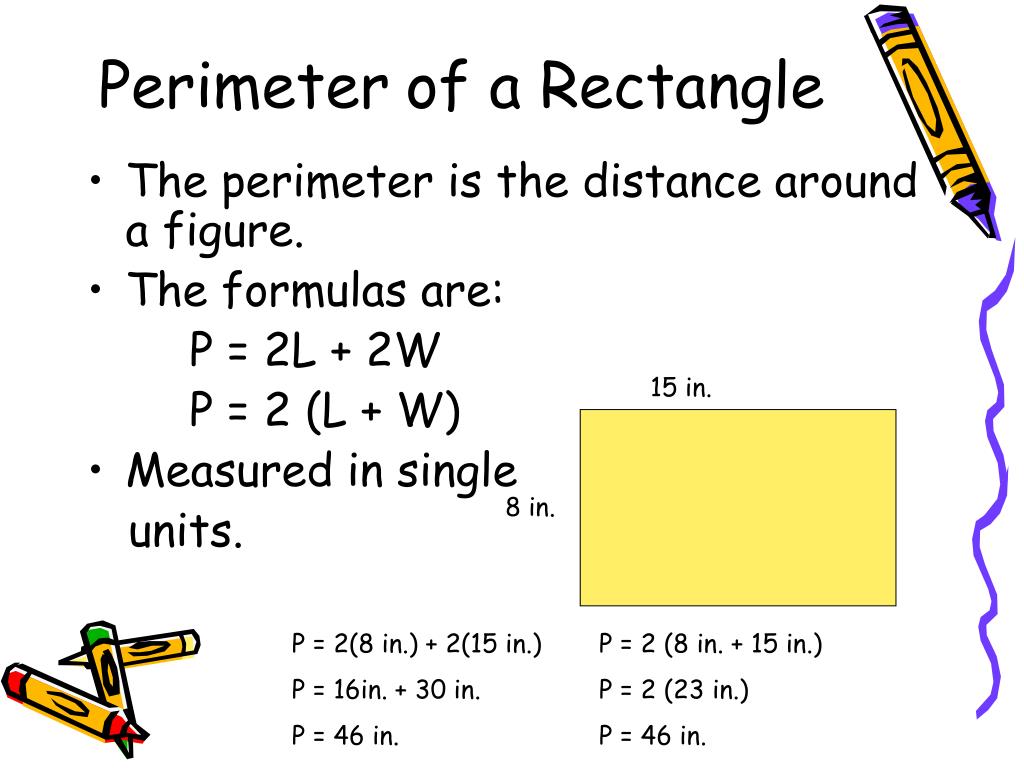
Since the length of the rectangle is given as 4cm, we can substitute, L with 4. We start with the formula for the perimeter of a rectangle, P=2(L+W). The next video will show some examples on using this formula.Īfter understanding the formula for the perimeter of a rectangle, let's see some examples on using the formula.įind the perimeter of this rectangle, when its length is 4cm, and its width is 3cm. Note that, in any calculation, when we found the value of P, it is important to include the unit.įor example, if L and W are given in centimeter, the unit for the perimeter will be in centimeter as well. Hence, by taking out '2', we have, 2(L+W).

Notice that, these two terms have '2' as a common factor. Since, the perimeter of the rectangle, P, is the total distance around the outside of the rectangle, the perimeter, will be equals to L, add with W, add with another L, and finally, add with another W. This rectangle has the length of L and the width of W.

In this lesson, we will learn about the perimeter of a rectangle.Ĭonsider this rectangle.


 0 kommentar(er)
0 kommentar(er)
